On utilise en mathématiques un ensemble de notations pour condenser et formaliser les énoncés et les démonstrations.
Quand deux traductions d'une notation sont données, l'une est la traduction mot-à-mot et l'autre est la traduction naturelle.
Le présent article traite des notations mathématiques latines. Il existe d'autres notations mathématiques non latines telles que la notation mathématique arabe moderne
Système hexadécimal à base 16 :
Le système de numération à base 16 (hexadécimal) permet de représenter les nombres binaires sous une forme plus lisible.
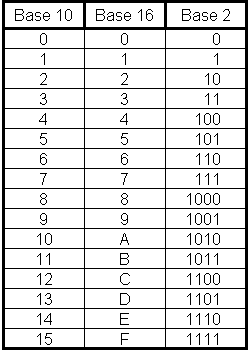
image : tableau – représentation hexadécimale
Les ordinateurs exécutent tous les calculs en mode binaire. Toutefois, il existe plusieurs situations dans lesquelles la valeur binaire renvoyée par un ordinateur est exprimée sous sa forme hexadécimale pour une lecture plus facile.
Ainsi, le registre de configuration des routeurs Cisco requiert souvent des conversions de valeurs hexadécimales en valeurs binaires et inversement. Les routeurs Cisco possèdent un registre de configuration d’une longueur de 16 bits. Un nombre binaire de 16 bits peut donc être représenté comme un nombre hexadécimal à quatre chiffres. Par exemple, le nombre binaire 0010000100000010 est égal à 2102 dans le système hexadécimal. Les nombres hexadécimaux ont souvent comme préfixe 0x. On écrira par exemple le nombre hexadécimal 2102 de la façon suivante : 0×2102.
Tout comme les systèmes binaire et décimal, la notation hexadécimale repose sur l’utilisation de symboles, de puissances et de rangs.
Les symboles utilisés sont les chiffres 0 à 9 et les lettres A à F.

image : conversion binaire-hexadécimal/hexadécimal-binaire
Pour représenter n’importe quelle combinaison de quatre chiffres binaires, il suffit d’un seul symbole hexadécimal, contre un à deux symboles décimaux. La représentation d’une combinaison de huit chiffres binaires requiert deux chiffres en format hexadécimal, tandis qu’elle peut en nécessiter jusqu’à trois dans le système décimal. Étant donné qu’un symbole hexadécimal représente toujours un nombre binaire de 4 bits, la représentation hexadécimale est plus simple d’utilisation lorsque l’on travaille avec de grands nombres binaires. Ceci réduit les risques de confusion liés à la lecture de longues chaînes de nombres binaires et l’espace requis pour écrire les nombres binaires. Rappelez-vous qu’il est possible d’utiliser les caractères 0x pour désigner une valeur hexadécimale. Le nombre hexadécimal 5D peut donc s’écrire 0x5D.
Pour convertir un nombre hexadécimal en nombre binaire, il suffit de remplacer chaque chiffre hexadécimal par son équivalent binaire de quatre bits.
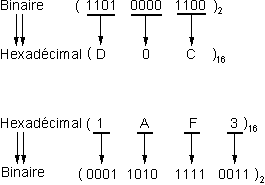
image : conversion hexadécimal/binaire
Logique booléenne ou binaire :
La logique booléenne appuie sur les circuits numériques qui peuvent accepter une ou deux entrées (tensions électriques).
 image : portes logiques (entrées/sorties)
image : portes logiques (entrées/sorties)
La tension de sortie générée dépend de la tension d’entrée. Pour les ordinateurs, les deux tensions possibles correspondent aux états En fonction et Hors fonction. A ces deux états sont associés les valeurs binaires un et zéro.
La logique booléenne est une logique binaire qui permet de comparer deux valeurs et d’effectuer un choix d’après ces valeurs. Ces choix reposent sur les opérations logiques ET, OU et NON. A l’exception de NON, les opérations booléennes remplissent la même fonction. Elles acceptent deux valeurs – 1 ou 0 – et génèrent un résultat d’après la règle de logique appliquée.
L’opération NON considère la valeur d’entrée et génère son opposé.
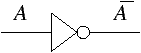
symbole de porte logique NON (NOT)
La valeur 1 donne 0 et inversement. Rappelons que les portes logiques sont des dispositifs électroniques conçus spécialement pour exécuter une fonction particulière. Pour la fonction NON, la règle logique appliquée consiste à générer, quelle que soit la valeur d’entrée, la valeur opposée en sortie.
L’opération ET compare deux valeurs d’entrée. Si les deux valeurs sont égales à 1, la porte logique génère la valeur de sortie 1. Sinon, elle renvoie la valeur 0. Il existe quatre combinaisons de valeurs d’entrée ; trois d’entre elles donnent 0 comme valeur de sortie de 0 et une seule génère la valeur 1.
image : symbole de porte logique ET (AND)
L’opération OU prend également en compte deux valeurs d’entrée.

image : symbole de porte logique OU (OR)
Si l’une d’elles au moins est égale à 1, alors la valeur de sortie est de 1. Comme pour l’opération ET, quatre combinaisons de valeurs d’entrée sont possibles. Trois de ces combinaisons donnent une valeur de sortie de 1, tandis que la quatrième génère un 0.

table de vérité pour la porte logique OU (OR)
Dans un réseau, deux types d’opérations font appel à la logique booléenne : la création de masques de sous-réseau et de masques génériques, qui permettent de filtrer des adresses. Utilisées pour identifier les équipements du réseau, les adresses peuvent être regroupées en plusieurs sous-ensembles ou contrôlées par des outils réseau différents.
Système de numération à base 2 :
Le système binaire comme le système décimal, utilise des symboles pour représenter les données. Deux symboles seulement sont utilisés par ce système, le 0 et le 1. Dans un nombre binaire lu de droite à gauche, le rang de chaque chiffre correspond à 2, le nombre de base, élevé à la puissance (exposant) 0, puis à la puissance 1 et ainsi de suite jusqu’à la puissance 7. Les valeurs respectives des rangs, de droite à gauche, sont donc les suivantes : 20, 21, 22, 23, 24, 25, 26 et 27, ou 1, 2, 4, 8, 16, 32, 64 et 128.
Voici un exemple:
101102 = (1 x 24 = 16) + (0 x 23 = 0) + (1 x 22 = 4) + (1 x 21 = 2) +
(0 x 20= 0) = 22 (16 + 0 + 4 + 2 + 0)
Cet exemple montre que le nombre 10110 en base 2 est égal au nombre décimal 22.
l’exemple si-dessous présente l’opération de conversion inverse :
image : exemple de conversion binaire d’un nombre décimal

Aucun commentaire:
Enregistrer un commentaire